The Design of Microwave Millimeter-Wave Control Components
JONAH ADELMAN, MEMBER, IEEE, RACHEL BEN-MICHAEL. SHIMON CASPI. AND SAMUEL HOPFER, LIFE FELLOW, IEEE
Abstract -The design of broad-band high-performance control components covering the 18-40 GHz frequency range utilizing microstrip technology is described. Design considerations and experimental results are presented for high-speed single-pole, single-throw and single-pole, doublethrow switches with 80 and 60 dB isolation, respectively. Design equations and experimental results are presented for a 3 dB quadrature microstrip reentrant coupler and for a nonreflective voltage-controlled microwave attenuator with a dynamic range of 50 dB.
I. Introduction
The well-known capabilities and potential advantages of millimeter (mm) wave systems have begun to be realized in the past several years. Of particular
importance is the 18-40 GHz region because of the relatively low atmospheric attenuation of electromagnetic waves in this region, as well as the presence of an atmospheric transmission window near 35 GHz. In addition, the 18-40 GHz range represents a natural extension of the traditional 1-18 GHz microwave region.
To realize microwave components in the 18-40 GHz region, several technologies are possible. The oldest technology is waveguide, which offers the advantages of low loss and high power-handling capability, but is cumbersome and not readily amenable to the integration required of modern microwave solid-state components, These shortcomings are partially overcome by the finline [1] technology developed by Meier and others, but difficulties remain in developing the broad range of high-performance microwave components and supercomponents required in modern mm-wave systems. A third approach is to utilize the planar transmission techniques used at lower frequencies. This approach can be implemented very successfully to yield 18-40 GHz components whose performance equals or approaches that of 8-18 GHz components. Although this approach can be extended beyond 40 GHz as well. performance will be limited by practical fabrication and assembly considerations.
This paper describes the design approach and experimental results achieved for broad-band solid-state control components covering the 18-40 GHz region. The components developed include:
- Single-pole, single-throw (SPST) switch with 80 dB isolation and 10 ns rise and fall times.
- Single-pole, double-throw (SPDT) switch with 60 dB isolation and 10 ns rise and fall times.
- 3 dB quadrature microstrip reentrant coupler [2].
- Nonreflective voltage-controlled attenuator (VCA) with 50 dB dynamic range.
The isolation and speed achieved for the switches exceed those reported for broad-band switches in this frequency range. An absorptive VCA for this frequency range has not, to our knowledge, been previously reported.
II. Design Approach
The transmission medium utilized in most lower frequency (1 -1 8 GHz) applications is a planar transmission line operating in the transverse electromagnetic (TEM) or quasi-TEM mode. The component interfaces to the outside world via a coaxial connector operating in the TEM mode. A major advantage of this approach is the ease with which discrete chip components such as diodes and transistors may be assembled and integrated using modern bonding and die attach techniques. An additional advantage is the extremely wide bandwidth of single-mode operation available, which extends from dc to the first appearance of a non-TEM mode. For a coaxial connector with outer diameter b, inner diameter a. and air dielectric. the first non-TEM mode is the TE11 mode and occurs approximately at [3]
λ ≈ π(a + b)/2
The recently developed Wiltron K™ 2.92 mm and Omni Spectra OS-50™ 2.4 mm connectors operate mode free to 46 GHz and more than 50 GHz. respectively. It is therefore possible, if proper care is exercised, to apply lower frequency techniques and approaches to the 18-40 GHz region as well. This has been the basic approach adopted in the work described in this paper.
The planar transmission medium chosen for the development of mm-wave solid-state control components is the microstrip line. For these components. it offers superior performance and ease of assembly when compared with alternative approaches. Since propagation in microstrip is only quasi-TEM in nature, dispersive effects can be significant. By choosing a thin substrate with low dielectric
constant, such as 0.005 in Duroid™ (manufactured by the Rogers Corporation), dispersive effects are minimized. In addition, the first occurrence of higher order microstrip modes will then be well beyond the frequency band of operation.
The transition from coaxial connector to microstrip line must be optimized to minimize reflections at the interface. The techniques utilized to optimize the transition are similar to those employed at lower frequencies and follow the general outlines suggested by the connector manufacturers. The capacitive discontinuities inherently present in the transition must be compensated by inductive sections of line (Fig. 1). In addition, precise fabrication and assembly techniques must be developed to meet the exacting tolerances required. Using these techniques, microstrip test fixtures were fabricated and tested from 0.1 to 40 GHz. The return loss for a pair of connectors separated by a 1 in microstrip line was better than 17 dB to 18 GHz and better than 14 dB to 40 GHz. These results are fairly close to theoretical expectations, particularly in the light of the fabrication and assembly tolerances present. The insertion loss of the fixture was as expected on theoretical grounds.
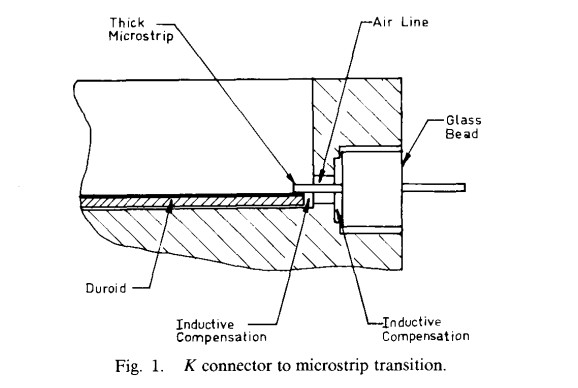
III. Switch Design and Experimental Results
SPTS Switch
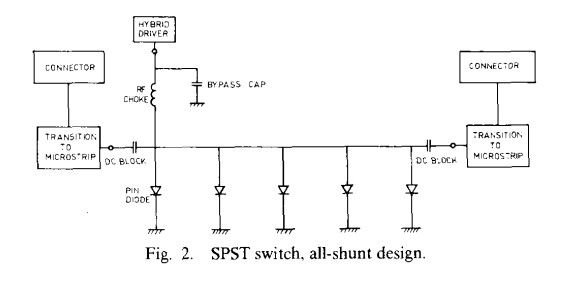
A block diagram of an all-shunt SPST utilizing p-i-n diodes is shown in Fig. 2. An all-shunt topology was chosen in order to meet the design goals of 80 dB isolation and 10 ns rise and fall times. The most critical aspect of the SPST design is the choice and assembly of the p-i-n diode, whose equivalent circuit is shown in Fig. 3. When the diode is in the OFF state, the inductance of the bonding ribbons together with the capacitance Cj of the diode forms an n = 3 low-pass filter [4]. If the characteristic impedance of the microstrip line is Z0, then an n =3 Chebyshev filter may be formed by choosing
L = g1Z0/wc
C = g2/(wcZ0)
where wc is the cutoff frequency of the filter and g1 and g2 the low-pass prototype values. At 40 GHz, the diode ribbon can no longer be treated as a lumped parameter, and the desired ribbon length is found by computer optimization.
A diode Cj of less than 0.07 pF is required to obtain a good match over the entire 18-40 GHz range. Such diodes are commercially available from most microwave
p-i-n diode manufacturers. Another significant parameter is the equivalent parallel resistance of the diode in the OFF state, since this gives rise to the approximately
0.4 dB insertion loss of the diode at 40 GHz. The primary physical mechanism responsible for this loss appears to be the complex, and therefore dissipative, nature of the dielectric constant of the swept-out “i” layer of the p-i-n diode.
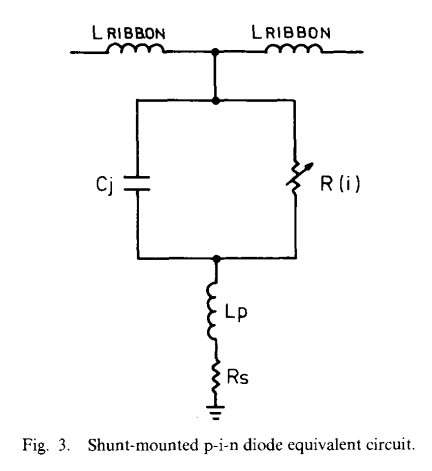
When the diode is in the ON state, R(i) is typically less than 2 Ω at 10 mA dc current, and the SPST switch is in isolation. At 40 GHz, however, the isolation of the SPST switch is limited by two other factors. One is the parasitic inductance Lp of the diode, whch derives primarily from the fact that the n+ region of the diode may be considered as a short length of low-impedance line which is short-circuited to ground. Lp is approximately 0.02 nH, which corresponds to a reactive impedance of 5 Ω at 40 GHz. An even more significant factor is the presence of non-TEM modes. To suppress the TE10 waveguide mode, the block must be channelized. Since the propagation of the TE10 mode in a waveguide of width a is given by [5]
γ10 = j [(2π/λ0)2 - (π/a)2]1/2
the channel dimensions must be chosen accordingly. Even after channelizing the block, however, the effect of non-TEM modes is not eliminated entirely since the modes are still launched and then reconverted to the TEM mode.
The design of the bias circuitry, particularly of the bias choke, presents difficulties for broad-band applications. One approach is to utilize miniature multiturn air coils. To first order, such a coil may be modeled [6] as a parallel L-C circuit, with the capacitance arising from the displacement current flowing between turns of the coil. This model has been found to be quite accurate up to and somewhat beyond the self-resonant frequency of the coil. Coils of this type have been fabricated and tested to 40 GHz with less than 0.1 dB insertion loss and better than 20 dB return loss when mounted in shunt across a 50 Ω microstrip transmission line.
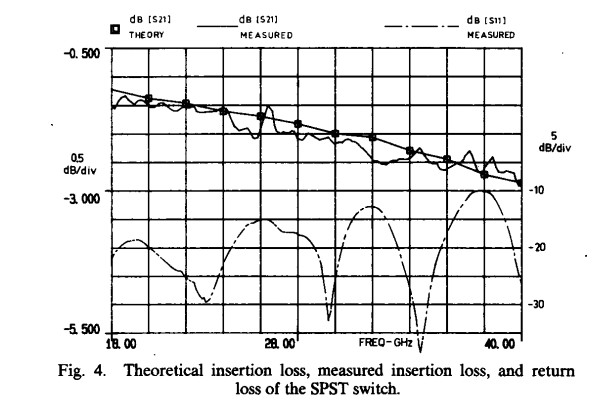
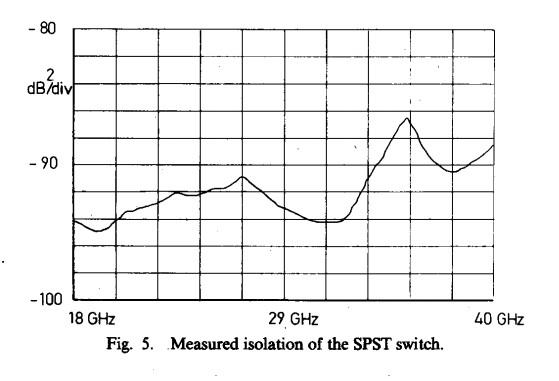
Based upon the above considerations, SPST’s were fabricated and then tested on the Wiltron 5669A scalar analyzer system. Isolation measurements, which require a dynamic range of greater than 80 dB, were performed using the Wiltron 6669A sweep generator, the EIP 578 sourcelocking microwave counter, and the HP 8566B spectrum analyzer, under the control of an HP 85B computer. In general, the experimental results achieved were in good agreement with those expected on theoretical grounds. A comparison of theoretical and measured insertion loss performance is provided in Fig. 4, as well as the measured return loss. The measured isolation performance is plotted in Fig. 5. The isolation is less than that prediced by a theoretical TEM model because of the presence of non-TEM leakage modes. The overall performance of the SPST switch is summarized in Table I.
B. SPDT Switch
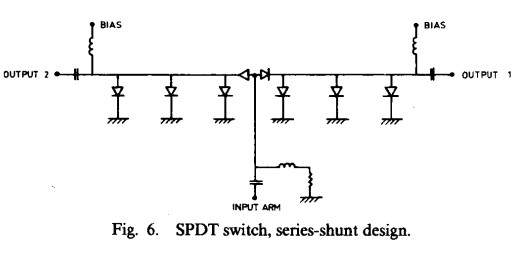
To achieve 60 dB isolation and 10 ns rise and fall times, a series-shunt topology was chosen (Fig. 6). Of particular importance is the design of the junction area. If one port of the SPDT is ON and the other is OFF, the capacitance of the series diode in the OFF arm loads the junction and must be compensated [7]. Although models exist in the literature for microstrip tee junctions, their accuracy at 40 GHz is questionable. The necessary inductive compensation was therefore arrived at by an initial computer analysis and subsequent experimental optimization. In addition, the isolation of the OFF arm as well as the return loss of the ON arm is degraded by the physical distance between the series beam lead diode and the shunt diode. To minimize this effect, the beam lead diode was bonded directly to the mesa of the shunt chip diode. A photograph of the internal construction of the SPDT switch is provided in Fig. 7. The performance of the switch is summarized in Table I.

IV. Quadrature 3 dB Microstrip Reentrant Coupler
Although the Lange [8] coupler is widely used at lower frequencies, its implementation in the 18-40 GHz range is problematic due to tight fabrication and assembly requirements. These problems are further compounded when a thin substrate with low dielectric constant is used. An alternative approach is the “Hopfer” coupler [2], which is a microstrip realization of Cohn’s [9] reentrant coupler. As shown in Fig. 8, the tight coupling is achieved by means of floating upper and lower shields in the coupled region. A major advantage of this structure is that it inherently ensures a 90° phase difference between direct and coupled arms. ‘This is of particular importance in components such as balanced attenuators and amplifiers, where the input match depends upon a 2 X 90° = 180° phase difference between signals. In addition, if a substrate with a low dielectric constant is used, the directivity is excellent because the phase velocities of the even and odd modes are nearly equal. Finally, fabrication and assembly are relatively straightforward and can be easily implemented on soft substrates such as Duroid.
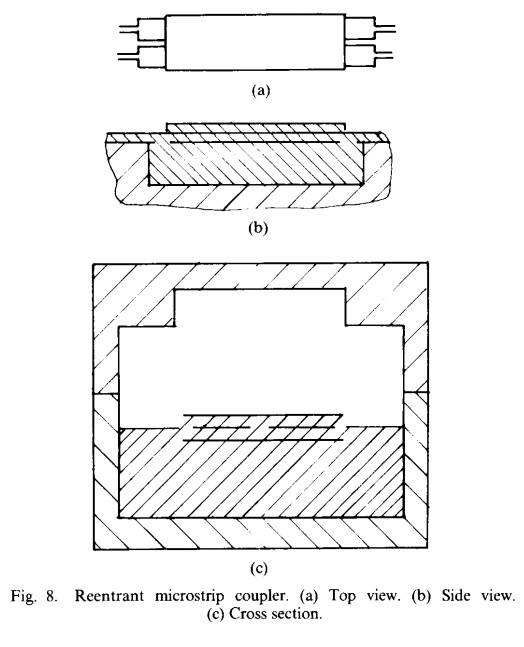
As described in [2], the Hopfer coupler can be described in terms of its odd- and even-mode impedances. To an excellent approximation, the odd mode is contained entirely within the stripline region of Fig. 8 and its impedance is equal to the odd-mode impedance of the coupled striplines. For the odd mode, the shields are at ground potential. For the even mode, the shields are floating, and the even-mode impedance is given approximately by
Z0e = Z ′0e + 2Z01
where Z ′0e is the even-mode impedance of the coupled striplines and Z01 is the impedance of the thick microstrip obtained by connecting upper and lower shields. The effective dielectric constant of the odd mode is equal to the dielectric constant, ∈r, of the substrate material. The effective dielectric constant of the even mode can be shown [10] to be equal to
∈eff = (Z ′0e √∈r + 2Z01 √∈01) / (Z ′0e / √∈r + 2Z01 / √∈01)
where ∈01 is the effective dielectric constant of the thick microstrip.
In extending the Hopfer coupler to the mm-wave region, a number of difficulties arise. The most serious problem is the suppression of undesired non-TEM modes. In particular, the TE10 waveguide mode must be suppressed, since its field structure lends itself readily to coupling into the TEM mode. By reducing the width, a, of the waveguide so that 2a is less than the wavelength of the highest frequency in the band, the TE10 mode may be cut off. However, the width cannot be reduced too greatly because the sidewalls of the channel begin approaching the upper and lower shields. To further increase the cutoff frequency of the TE10 mode, the upper ground plane may be relieved, thus forming an “inverted” ridged waveguide. As shown in [11], the cutoff frequency is thereby increased by up to 15 percent. The sidewall proximity to the coupled lines adds capacitance to the thick microstrip line and must be included in the calculation of Z01. To first order, the capacitive effect at each edge of the line is the same as the fringing field to the equivalent electric wall separating the odd mode of two coupled microstrip lines, for which closed-form expressions exist. Z01 may then be approximated by
Z01 = Z ′01 Z00 / (2Z ′01 - Z00)
where Z ′01 is the thick microstrip impedance and Z00 is the odd-mode impedance of a pair of thick microstrip lines separated by twice the distance from the thick microstrip line to the sidewall. Since the thick microstrip line is relatively far from the lower ground plane, dispersive effects are no longer negligible and must be included. They are calculated using the closed-form expressions given in [12]. Finally, as in the lower frequency case, the inductive end portions of the coupled sections must be compensated capacitively.
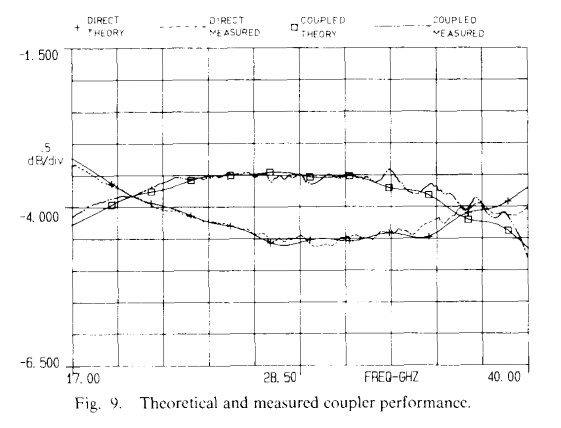
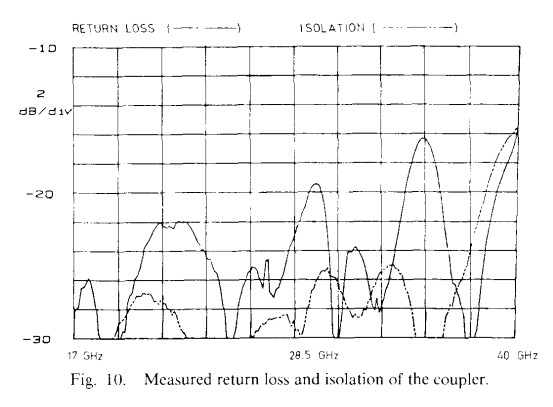
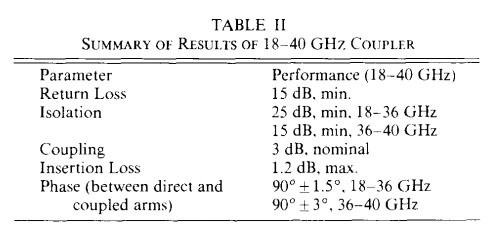
A computer program was developed including all the factors mentioned above, and the overall circuit was optimized and analyzed. Based on this, 18-40 GHz couplers were fabricated and tested. The results obtained are shown in Figs. 9 and 10 and are summarized in Table 2. As seen from Fig. 9. the measured coupling is in excellent agreement with theoretical expectations. The insertion loss of the coupler itself is less than 0.2 dB, with the additional 1 dB of loss arising from the approximately 1 in length of microstrip line in the test fixture between the connectors and the coupled region. As seen from Fig. 10, isolation is better than 25 dB to 36 GHz and 15 dB to 40 GHz, and the return loss is better than 15 dB across the entire band. One of the limiting factors in isolation and return loss performance is the coax-to-microstrip transition, which itself has a return loss of 20 dB at the high end of the frequency range. The phase between arms was measured on the Wiltron 360 vector network analyzer and is given in Table 2.
V. Nonreflective Voltage-Controlled Attenuator (VCA)
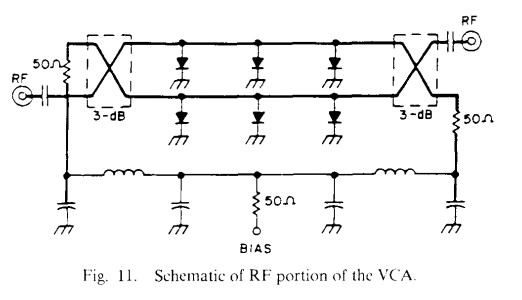
To obtain a nonreflective VCA covering the entire 18-40 GHz band with 50 dB dynamic range, a balanced approach [13] is taken, as shown in Fig. 11. The quadrature property of the coupler is critical here, since any deviation from quadrature results in a mismach at the input for high attenuation levels. For an ideal quadrature coupler, the direct and coupled transmission coefficients at center frequency are given, respectively, by [9]
ΓIN = (S11)coupler - (2c2 - 1)e-j2Θ1 + Γterminatione-j4Θ1
where Θ1 is the electrical length between the coupler output and the first shunt p-i-n diode at center frequency. (The second-order effect of the finite directivity of the coupler has been neglected.) To minimize the reflection of the 50 Ω termination, the physical size of the termination must be minimized and capacitive compensation introduced.
Two further aspects of the 18-40 GHz VCA design requiring attention are flatness of attenuation over the frequency band and linearization of attenuation as a function
of input voltage. For high attenuation levels, the attenuation as a function of frequency is given, to first order, by
S21 ≈ gn11(sinn - 1Θ) /2
where g is the normalized admittance of the conducting p-i-n diode. n is the number of shunt p-i-ti diodes and Θ is the spacing between diodes. For n = 3, this would imply a theoretical flatness of +=1.6 dB if the diode spacing were 90° at center frequency and g were independent of frequency. In practice, however, two additional factors must be taken into consideration. To begin with, as seen from
Fig. 3, g is frequency dependent; in fact, the inductance dominates at higher frequencies. In addition, since the attenuation level is defined relative to insertion loss, which varies with frequency, the overall flatness of attenuation versus frequency is affected. A computer program was therefore written to analyze and optimize the attenuator flatness. It was found that by reducing the impedance level
in the diode array, the flatness was improved. To obtain a linear attenuation versus voltage characteristic from the nonlinear attenuation versus current transfer function, p-i-n diodes with an appropriate resistance-current relationship were selected and existing low-frequency driver circuitry was slightly modified.
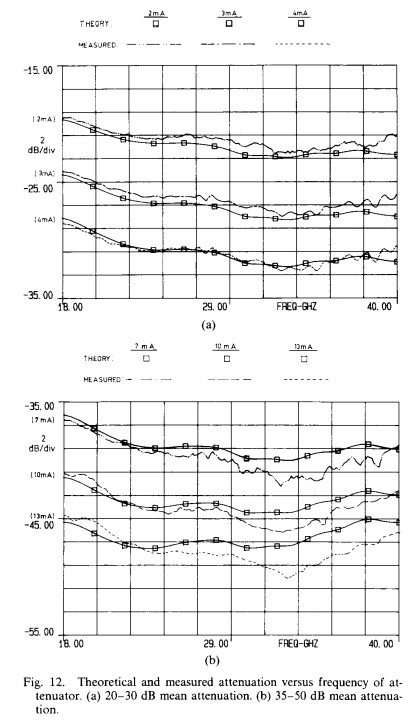
Utilizing the above approach, 18-40 GHz VCA’s were fabricated and tested. As shown in Fig. 12, the measured attenuation performance is close to that predicted on theoretical grounds, although there is some deviation at high attenuation levels. The VSWR was better than 2: 1 over the entire band for all attenuation settings, and the insertion loss was less than 4.0 dB to 40 GHz. A photograph of the internal construction of the completed unit is provided in Fig. 13.

VI. Summary
An approach has been presented for the design of broad-band solid-state control components covering the 18-40 GHz range. Theoretical and experimental results have been presented for the design and performance of an SPST switch, an SPDT switch, a 3 dB quadrature microstrip coupler, and a nonreflective VCA. The results achieved equal or exceed those reported thus far in the literature. Further development is planned to extend the bandwidth of the components developed as well as to develop additional control components such as phase shifters and frequency translators.
Acknowledgments
The authors wish to thank A. Gorbatte for his invaluable contributions to this project and for supervising the mechanical design of the components, Y. Epstein for painstakingly assembling them, and S. Shlosberg for testing, debugging, and improving them.
References
[1] P. J. Meier, “Integrated finline millimeter components,” IEEE
Trans. Microwave Theory Tech.. vol. MTl-22. pp. 1209-1216, Dec.
1974.
[2] S. Hopfer. “A hybrid coupler for microstrip configuration.” in 1979
Int. Microwave Symp. Dig., pp. 428-430.
[3] N. Marcuvitz, Waveguide Handbook. New York: McGraw-Hill,
1951, p. 77.
[4] R. V. Gamer, Microwave Diode Control Devices. Norwood. MA:
Artech, 19’76, ch. 5 and 6.
[5] R. E. Collin, Foundations /or Microwave Engineering. New York:
McGraw-Hill. 1966, ch. 3.
[6] J. Adelman. “Technical report on multi-turn coils,” General Microwave
Corp., Amityville, NY, Tech. Note, Mar. 1982.
[7] R. V. Carver, Microwave Diode Control Devices. Nonvood, MA:
Artech, 1976, ch. 7.
[8] J. Lange, “Interdigitated stripline quadrature hybrid,” IEEE Truns.
Microwsave Theon. Tech., vol. MTl-17. pp. 1150-1151. Dec. 1969
[9] G. Matthaei, L. Young, and E. M. T. Jones, Microwave Filters,
lmpedance-Matching Networks and Coupling Structure;,. Nonvood,MA: Artech, 1980, eh. 13.
[10] Z. Adler, “Analysis of Hopfer coupler with improved accuracy,”
General Microwave Corp., Amityville, NY. Tech. Note, Aug. 1984.
[11] J. P. Roth and K. Ishi, “The cutoff characteristics of the channel
waveguide,” IEEE Trans. Microwave Theory Tech., vol. M’M ~ 12,
pp. 245-247, Mar. 1964.
[12] E. Hammerstad and 0. Jensen, “Accurate models for microstrip
computer-aided design,” in 1980 lnt. Microwave Srmp. Dig., pp.
407-409.
[13] J. F. White, Microwave Semiconductor Engineering. New York:
Van Nostrand Reinhold, 1982, ch. 9.
Jonah Adelman (M’86) was born in Brooklyn, NY, on October 25, 1950 He received the B S degree (summa cum laude) in mathematics and physics in 1971 from Brooklyn College In 1973 he received the M S degree in applied mathematics
from New York University, New York. NY, where he performed doctoral research in
magneto-fluid dynamics from 1973 to 1976 From 1976 to 1978 he was a Lecturer of Mathematics at John Jay College From 1978 to 1983 he worked at General Microwave Corporation as a Research and Development Engineer. where he was engaged in the design and development of microwave solid-state control components and supercomponents In 1983 he moved to Israel, where he joined Tadiran Ltd as the Manager of its Microwave Integrated Circuit Department In 1985 he assisted in the establishment of the General Microwave Israel Corporation, Jerusalem, Israel, and became Its Director of Engineering His current research activities are the supervision of the development of mm-wave solid-state components and supercomponents and of microwave VCO’s, DTO’s, and DRO’s.
Rachel Ben-Michael was born in Jerusalem, Israel, on November 9, 1959. She received the B.Sc. (honors) degree in 1982 from the Israel Instituet of Technology, Hafia, Israel. From 11983 to 1985, she worked as a Research Engineer at the Israel Ministry of Defense ("Rafel"), where she was engaged in the design and development of microwave switches, filters, and finline components. In 1985 she joined the General Microwave Israel Corporation, Jerusalem, Israel, where she is currently engaged in the design and development of mm-wave control compenents and super compoenents.
Shimon Cad was born in Tel Aviv. Israel. on March 31. 14.50 He received the B Sc degree in 1978 from the Israel Institute of Technology Haifa. Israel From 1978 to 1985 he worked as a Microwave Engineer at Elta. a subsidian of Israel Aircraft Industries. where he was engaged in the design and development of microwave passive components. In 1985 he joined the General Microwave
Israel Corporation. Jerusalem, Israel. where he is currently involved in the design of mm-wave control components and supercomponents.
Samuel Hopfer (SM’jX-F’82-LF’87) was born in Remngen. Germany. on November 21, 1914 He received the B.A. degree from West Virginia University, Morgantown, WV, in 1944, the M.A. degree from Cornell University, Itahaca. NY. in 1945, and the Ph.D. degree from the Polytechnic Institute of Brooklyn, Brooklyn, NY. in 1954.
He joined P.R.D. Electronics in 1945, advancing to the position of Manager of Research in 1960 In 1963 he joined the General Microwave Corporation as Vice Preisdent and Director of Reasearch and Development. In 1983 he emigrated to Israel, where he took part in the establisment of the General Microwave Israel Corporation, Jerusalem, Israel, serving as its technical consultant. Among his numerous contributions to the microwave field are his work on the theory of coupling in the multimode systems, the development of broad-band transmission systems, the design of thin-film thermoelectric power mether, and the development of broad-band microwave radation probes. He has served for many years as Adjunct Professor of Electrical Engineering at the Polytechnic Institute of Brooklyn. Dr. Hopfer is a member of the New York Academy of Sciences, the American Physical Society, and Sigma Xi.
